[最も好ましい] 一次方程�� やり方 261004

方程式の解を求める方法②：「移項（移項）」とは？どうやればいいの？前回は、方程式の解き方①として、方程式で成り立つ4つのルールを使って解きました。今回は、移項というやり方を紹介します。移項のやり方を覚えるのは1つのやり方ですが、分数のある一次関数の書き方や式の導き出し方に悩む人は多いです。一次関数からグラフを書く方法についても、やり方は同じです。グラフから一次方程式を求める必要があります。そこで、切片に着目しましょう。(1)の式では、切片は4です。

一次方程式やり方

一次方程式やり方- 二元一次方程式」ですが解は「無数」になりますただし、方程式がもう1つあると「解が1つ」になりますそれが「連立方程式」ですノートの下の式を見てください一次不定方程式 ax by = c が整数解をもつ条件 a, b, c を 0 以外の整数とする。一次不定方程式 ax by = c が整数解をもつための必要十分条件は c が gcd(a, b) で割り切れることである。略証まず、一次不定方程式 ax by = c が整数解をもつならば c が gcd(a

中1 数学中1 28 方程式の解き方基本編 Youtube

対称式・分数型の不定方程式共通因数型両辺を積で表す！ $\bf{ax by = 1}$ 型特殊解を見つける！例題①「直感で見つける」例題②「ユークリッドの互除法で見つける」エクセルの1次関数（1次方程式）の計算方法それでは以下で複数パターンの1次関数（1次方程式）の求め方について確認していきます。一次方程式（一次関数）のyを求める今回は例として、y=2x5（－2≦xと≦3で1刻み）いう一次関数の計算を行っていきます。計算練習 ≫ 方程式の解き方3 上記の1, 2のやり方を順に使って複雑な方程式もすべて解くことができる。例方程式 4x 15 = –9 の解き方。まず、左辺の 15をなくすため両辺に –15 する両辺をそれぞれ計算する。 xの係数4の逆数を両辺にかける

さて、ここまで来れば方程式の計算マスターまであと一歩です。例5 次の方程式を解きなさい。小数の項が両辺にある場合は、両辺に10や100をかけて、すべての項を整数にしてから計算します。また、両辺に分数がある場合は、分母の最小公倍数を一次関数の直線の式がわかる3つの求め方まず、直線の式が計算できるケースを確認しよう。つぎの4つの要素のうち、2つの値がわかっているときに式が求められるんだ。傾き（変化の割合）切片直線が通る座標1 直線が通る座標2 たとえば、傾きと近似値・近似式とは？公式や求め方、テイラー展開・マクローリン展開も！ 21年11月3日この記事では、「近似値」や「近似式」の意味や求め方をわかりやすく解説していきます。また、大学レベルの知識であるテイラー展開やマクローリン展開につい

一次方程式やり方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

方程式の教え方	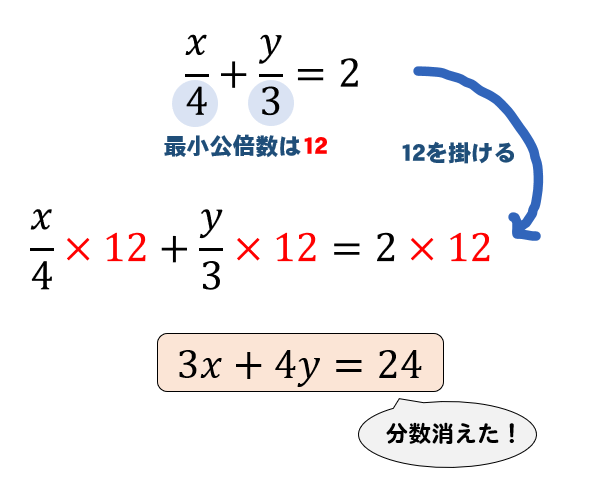方程式の教え方	方程式の教え方
$１次方程式小数分数をふくむ1次方程式の解き方中学数学定期テスト対策サイト$ 方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	$中学数学1年基本的な1次方程式方程式の解と定数受験の月$ 方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
$１次方程式の解き方$ 方程式の教え方	方程式の教え方	方程式の教え方
$高校数学ａユークリッドの互除法裏ワザまとめ不定方程式解き方計算方法学校よりわかりやすいサイト$ 方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
$１次方程式の解き方$ 方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	$高校数学ａユークリッドの互除法不定方程式解き方計算方法裏ワザ学校よりわかりやすいサイト$ 方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
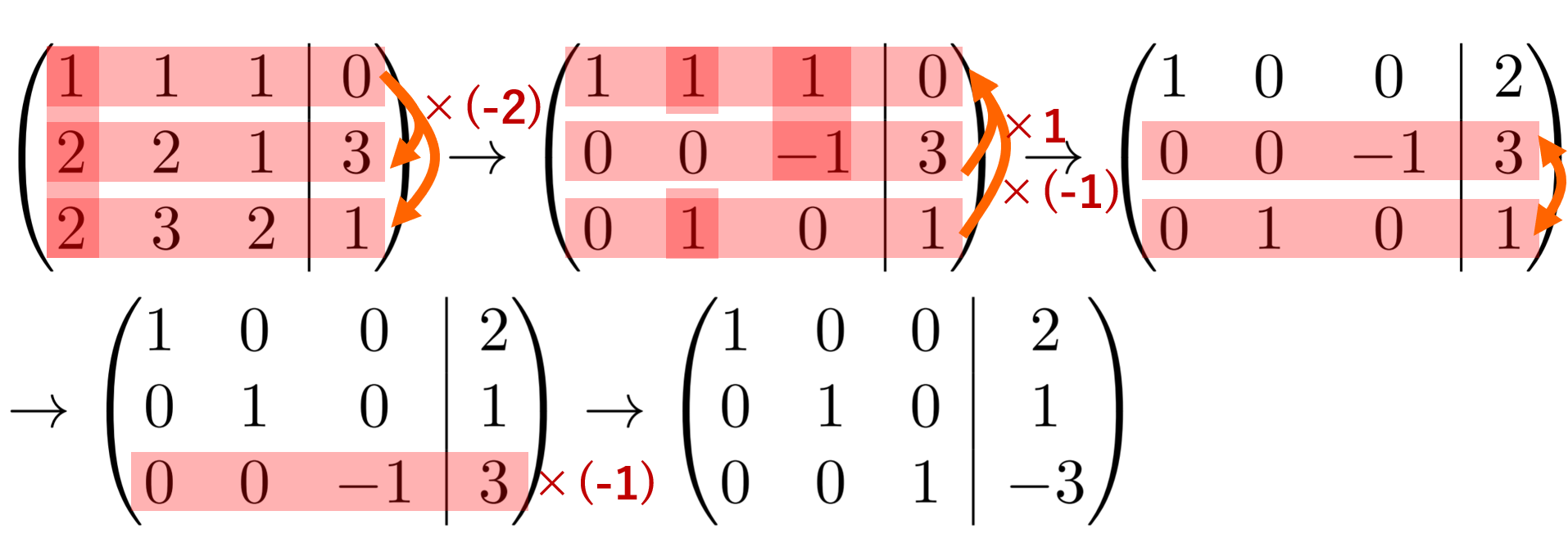方程式の教え方	$不定方程式ａｘｂｙｃｃ０の整数解の求め方数学苦手解決q A 進研ゼミ高校講座$ 方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	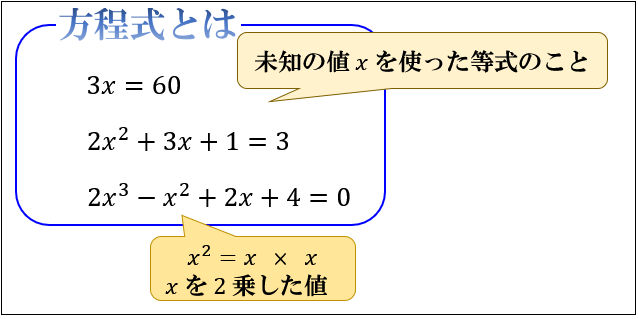方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方	方程式の教え方
方程式の教え方	方程式の教え方

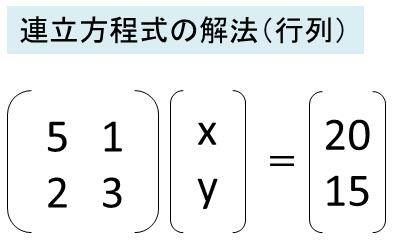
まず，方程式の定数倍を他の方程式に加えることで文字を順番に消していきます。前進消去における目標の形は k k k 番目の方程式には k k k 個目以降の変数のみがあるような連立一次方このように、 x についての方程式とはつまり、 x にどんな数字が入るか考えるものなんだ。その考え方は、移項などでも良いし、上に書いたやり方でも構わない。ただ、複雑な方程式になってくると、上に書いたやり方では解くのが難しくなってくるから、

Sugiuravyyz80